量子力学速成版*

理清概念

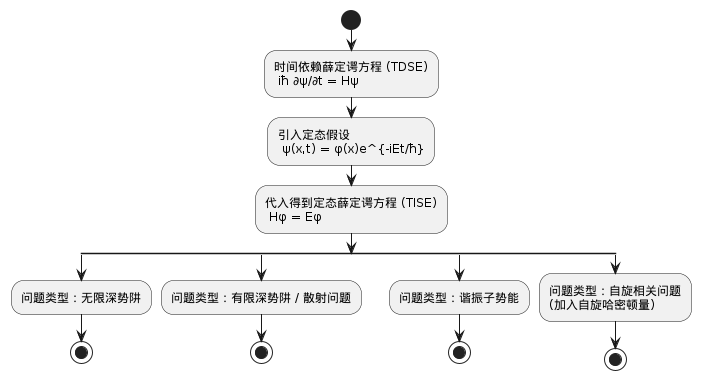
物理规律如何描述？我们可以把想研究的对象每一个状态表达出来，这样想知道什么就查看对应状态即可，因此我们来研究的是状态。 量子力学中，状态被封装在函数里，即波函数 \(\psi(x,t)\) .随时间演化满足薛定谔方程（在教材中这被作为假设）：

\begin{equation*} ih\dot{\psi}=H \psi \end{equation*}

H 是哈密顿算符，这个方程被认为等价于量子力学的牛顿方程。

下面解释 算符 ： 为了满足实验中物理量只能取固定值的现象（这也是量子物理的初衷），使用线性代数特征值（还有波动概念，波节也是整数化的这一点另谈），即可测量的物理量变成了（（厄米）矩阵）算符，算符乘上波函数得到了改物理量的值。 厄米矩阵保证了取值为实数。

换一种说法，就是我们有了状态，但我们怎么像原来经典力学一样知道这个对象现在位置速度呢，很简单你用对应算符（位置动量能量……）作用到态函数上就得到一个值，此即所求物理量。

\begin{gather*} H| \psi\rangle=\lambda \psi \end{gather*}

线代中的 矢量 \(\mathbf{a}\) 似乎和量力 \(|\psi\rangle\) 不同，其实只是换了一套符号：

• \(|\psi\rangle\) 右矢就是一般的列向量，可以表示波函数等等（向量表示函数，这里向量是在 Hilbert 空间，即无限维度的 Euclid 空间，Euclid 空间是有内积的线性空间）。所以量力中，向量和函数同样的（值得思考的问题：什么是向量，向量就是箭头吗）
• \(\langle\psi|\) 左矢则是右矢转置，数学上这两者是对偶空间关系。

个人认为使用左矢和右矢只是方便，方括号看多了觉得很规整。英文中左右分别叫 bra,(c),ket

于是可以得知， \(\left\langle \psi \right|\psi \rangle\) 得到数， \(\left\langle \psi \right|\psi \rangle\) 得到矩阵

量子力学成立时吊诡之处就是波动方程的解无法消除虚数部分（虚数的来源是……），为此波恩做出著名波恩诠释：波函数的模平方为粒子概率。

塌缩 collapse 指的就是算符乘波函数得到了实数值（没有任何神秘之处，因为所有信息本来多都蕴含在波函数里面）

接下来有了很多算符，我们会介绍算符互易性，也就是可交换性。之所以研究这个，是因为我们发现有些算符可以共享特征向量。如果可以找到一个范围内 CSCO：

量子力学后半部分繁复的点在于它用到了许多（所谓数学物理方法）特殊函数和结论，一般课程直接提供或记住即可。 如：厄米多项式

---

或称之为做题技巧