抽象之路笔记-
目前不适合看发布以调试
修订
着重补齐
太震撼,进展到第五讲感到很不简单可能要歇歇(结成浩你能不能写点这些代数的内容)
1. 内容介绍
梳理: 以人物串联的发展史
- 解方程历史
- 高斯之前
- 第三讲群论初步
- 第四讲尺规作图出发:域扩张、 Galois
- 第五讲环内容
- Kummer 的工作
- 青春理想
- 类域论
简介:
- 官方:
讲代数的历史,包括很多人文性内容如时代背景、历史变迁、横向对应
本短课程的主要目的是从数学发展史的观点,对代数和数论抽象化的历程,包括代数思想/概念/方法的发展史作一个简单介绍。
课程内容包括:
I. 从古巴比伦人求解一元二次方程开始,介绍求根公式的发展历程,包括意大利人的戏剧故事和阿贝尔、伽罗瓦的传奇。
2 ,介绍群论和伽罗瓦理论的基本思想和简单应用。
3 ,介绍数论从欧几里得到高斯的发展史。
4 ,介绍 Kummer 之前费马大定理的探索历程。
5 , Kummer 对于费马大定理的探索如何促成理想概念的引入、交换环论和代数数论的诞生。
6 ,类域论和抽象代数的建立。
一次笔记尝试、算是看过一些基本代数包括数学女孩后的兴之所至吧。
2. 代数
讲座说一说数学家从会算到不会算的历程:对数字理解不断加深、发现更多关于数的秘密(无穷无尽定理)的过程。
2.1. 古巴比伦
这是两河(幼发拉底河与底格里斯河)流域的文明, 公元前1900-前1600,汉谟拉比法典诞生之地方;对应夏朝。 楔形文字 cuneiform 写在泥板上;
数学能力:
- 二次方程的求解 \(ax^2+bx+c=0\)
使用60进制,1-60 60-80 80-99 4*20+10+9
归功于 Francois thureau-Danigin 法国人 和 Otto Neugebauer 破解 BM13901 大英博物馆 BM 藏品
- 勾股数组
在中国商高定理、勾三股四弦五
考古发现泥板上记载了巨大的勾股数,如 \((12709,13500,18541)\quad (2291,2700,3541)\) 哥伦比亚大学 Plimpton 322 (Plimpton赠与的322号) ,Otto 和 Sachs 破译
如此巨大的数推测当时人应当知道公式。
中国已知证明:可从古代图像看出
例子 13901 问题2: 正方形面积-边长=1430,求边长 此处 等价于问 \(x^2-x=870\)
解答: \(x^2-bx=c\)
| 步骤 | 说明 | 字母表示 | 结果 |
|---|---|---|---|
| 1 | 写下系数1 | b | 1 |
| 2 | 取一半 | \(\frac{b}{2}\) | |
| 3 | 取平方 | \(\left( \frac{b}{2} \right)^2\) | 1 |
| 4 | 加上870(c) | \(\left( \frac{b}{2} \right)^2+c\) | |
| 5 | 这是 \(29 \frac{1}{2}\) 的平方(开根号) | \(\sqrt{\left( \frac{b}{2} \right)^2+c}\) | \(29 \frac{1}{2}\) |
| 6 | 加上0.30 |
一步一步教过程
322 \(a^2+b^2=c^2 \Rightarrow \left( \frac{a}{c} \right)^2+\left( \frac{b}{c} \right)^2=1\) 取单位元 \(x^2+y^2=1\) 交点坐标
\(k\rightarrow (\frac{k^2-1}{k^2+1},\frac{2k}{k^2+1})\) 取 \(k=\frac{m}{n}\) 得到 \((\frac{m^2-n^2}{m^2+n^2},\frac{2mn}{m^2+n^2})\) 于是得到勾股数组: \((m^2-n^2,2mn,m^2+n^2)\) 得到本原的解
\(k=\{\frac{12}{5},\frac{64}{27},\frac{125}{54},\frac{9}{5},\dots\}\) 对注意到 \(m,n=2^i3^j5^k\) 原因:60进制
失传空白
Otto Neugebauer 只与数论波尔(尼耳斯波尔弟弟)发表一篇纯数学论文,主要是 创立 Zentrablatt Math(1931), 哥廷根。 希特勒上台在美国创立 Math Reviews(1939)
数学评论:
数学评论不应当和文章质量成正比。
好文章:大家都去读吧;
伟大数学家犯错误比末流数学家发现概率大。不应当忽视小数学家的贡献
张载(1020-1077)长安:为… 数学应当为往圣继绝学,传承。
我想更应该取理解发掘,因为传承下来总是存在前人的删减,而可能删去了一些非凡之处
2.2. 欧几里德
Ευκλειδης 几何学之父
生平: 约公元前330年—公元前275年 ——长平之战赵襄王,秦始皇之前
2.2.1. 《几何原本》 Elements
(应当就叫原本) 西方科学数学基础
不赞同降低小学难度,需要建立好良好的逻辑体系
几何为主的世界缘故: 我认为这是因为古希腊人对数的观念有关
《几何原本》同时是数论的起源:
13章 7-9章自然数整数的理论。
- 欧几里德引理 若素数 p|ab 素性(定义素理想等等的根源)可以直接推得 算数基本定义 高斯最先证明 整数的唯一分解性质
- 欧几里德第二定理:素数有无穷多 证明:假设素数哥舒有限,有 \(p_1,\dots, p_n\) 令 \(N=p_1\cdots p_n+1\) 则N 与\(p_1,\dots, p_n\) 互素,矛盾。反证成立。
历史上第一个关于无穷的结果
关注几何,于是对测量天文观测感兴趣,有 古典几何的三大难题
- 化圆为方
- 三等分角
- 立方倍体
归化为代数问题,如果有 在范围内的解就可以做
1837 1,3 1882 -2
2.3. 丢番图 Diophantus
被称为代数学之父 I (总共有3个人都获得此称号)
生平为200-284 ——三国时代~ 对应中国(可谓成就最大)数学家刘徽(225-295)
2.3.1. 《算数》
著作: Arithmetica 130个问题 他的年龄是根据数 6 12 7
当时著作往往是问题集,例如《海岛算经》、《孙子算经》
丢番图方程/不定方程进行广泛研究, 研究称为丢番图分析
例如 A=2a+1,求 \(x,y\in \mathbb{Q}\) \(x^2+y^2=A,\quad x^2,y^2>a\)
圆上作直线
- 研究三类二次方程
当时没有0,负数用的很少因此这样书写(才符合当时可以接受的形式)
(对应几何的思维方式)
可以想到如今我们感到负数自然便捷,而它本身恰恰也是一种符号的发明创造:
应用合适的概念有时候可促使研究更方便
中世纪 古希腊失掉 此时没有完全失传 重新连上
线性同余数方程
2.4. 阿拉伯数学
2.4.1. 花剌子模
Mohammad ibnmussa al-khwarizmi (780-850)(成吉思汗屠城)
唐朝晚期 波斯人
首都巴格达智慧宫,研究数学、航海
文艺复兴从阿拉伯文成新翻译回来
著作: al-Jabar 代数
这个词的含义是一步一步的操作
12世纪中叶
- 引入印度数字(即阿拉伯数字)
- 拉丁写法: algorism,algoritmi=algrothm
2500年前的事情重做一遍
2.4.2. al Karaji
- 将代数从几何图形运算操作中解决出来,出现四则运算
- 同余数问题 有有理直角三角形(边长是有理数)边长 \(a,b,c\in \mathbb{Q}\) ,面积 \(n=\frac{1}{2}ab\) 找出所有整数 n. 等价于 对于怎样 n 有 \(\exists a\in Q\) 使得 \(a^2\pm n\) 也是有理平方数 \((a,b,c)\rightarrow (\left( \frac{c}{2} \right)^2-n, \left( \frac{c}{2} \right)^2, \left( \frac{c}{2} \right)^2+n)=(\left( \frac{a-b}{2} \right)^2, \left( \frac{c}{2} \right)^2,\left( \frac{a-b}{2} \right)^2)\) 等价于(现代数学研究) \(y^2=x^3-n^2x\) 椭圆曲线 有 \((x,y) \quad x,y\in \mathbb{Q}\quad y\neq 0\)
2.5. 三次四次方程的求根方程
16世纪(文艺复兴全盛期,后三杰活跃时期)意大利人的成就
历史背景: 城邦国家:米兰公国、威尼斯共和国、佛罗伦萨共和国(文艺复兴的中心)
在意大利北部 (1870现代意大利的国家 世界第一所大学: Bologue 大学1088 世界大学之母(校训) 12世纪 巴黎大学、帕洛瓦大学(意大利) 王安石去世两年后
2.5.1. del Ferro(1465-1526)
Bologue 大学教授 1515 发现三次方程公式,未发表 1525 告诉学生 Fior 菲奥尔, dello Nave(女婿+学生) 给了一本笔记本记录了求解思路过程 针对方程:
\begin{align*} \label{eq:1} \text{I} \quad&x^3+px=q\\ \text{II} \quad &x^3=px+q \quad p,q\neq 0 \end{align*}fior 会 I
2.5.2. Tartaglia 塔塔利亚(1500-1557)
威尼斯共和国 Brescia 人
名字是一个蔑称,表示口吃。1512 与法国交战负伤所致。 自学成才,教学为生 一生潦倒,有钱就投入自己喜欢的军事研究,尤其大炮
2.5.3. 决斗:互相出题
Fior 自得为唯一传人,认为塔塔利亚虚名不实或者剽窃,发起挑战:
1535.2.22开始,双方各出30题,两个月时间求解
1535.2.13凌晨 塔塔利亚钻研出两种方程的解法。随后自己出题类型包含 I 和 II 。 而 Fior 只出他会的 I ,于是塔塔利亚一小时解出所有题,大获全胜。
2.5.4. Cardano/Cardan 卡尔丹诺(1501-1576)
米兰大公国 医生、星象学家。在社交中 长袖善舞。 治好苏格兰大主教 大逆不道上帝星座被赦免
赌博(出千的技术),作家
自己写信给塔塔利亚,承诺将对方介绍给米兰的西班牙总督,资助他继续军事研究。同时自己永不发表结果。
唯一在场是 Cardano 学生: Ferrari
5 Ferrari 1540 发现四次方程的解法 Ferriari 天才聪颖 Cardano 写书 Ars Magna (The Great Art) 1543 della Navr 邀请 1545 出版,记录了
文艺复兴最重要的数学著作 1546 塔塔利亚自己出版
2.5.5. Ferrari (1522-1565)
14岁作为Cardano学徒 之后作Bologue 大学教授 早逝 Cardano 生命短暂不要期望他们取悦你
塔塔利亚 \(x=u+v\)
\begin{equation} \label{eq:2} \begin{split} u^3+v^3=-q \\ uv=-\frac{p}{3} \end{split} \end{equation}四次方程:
\begin{equation} \label{eq:3} x^4+px^2+qx+r=0 \end{equation}令 \(z=x^2+y\)
\begin{equation} \label{eq:4} \Delta = q^2-4()() \end{equation}三次方程
副产物:虚数的诞生
\begin{equation} \label{eq:5} \Delta=\frac{q^2}{4}+\frac{p^3}{27} \end{equation}\(\Delta<0\) 三次求根无意义 例: \(x^3-15x-4=0\) Ars Magna 引入复数 Ra Algrbra(使用拉丁文引入代数) 包含:丢番图、 介绍复数的运算法则
复分析:可视化
3. 2
文艺复兴结束的人物:
3.1. 韦达
(1540-)
1591《解析艺术引论》,使用现代的数学符号 xyz abc 符号运算 韦达定理:总结三次四次根与系数的关系
\begin{equation} \label{eq:6} \begin{split} x^n+a_1x^{n-1}+\cdots+a_{n-1}x+a_n \\ =(x-x_1)\cdots(x-x_n)\\ \end{split} \end{equation} \begin{equation} \label{eq:7} a_k=(-1)^k \sum\limits_{1过来知道系数如何知道根(伽罗瓦)
传奇人生:
- 破译密码:帮助法国国王赢得对西班牙的战争 代数与数论的应用
- 芬兰数学家挑战,要求法国国王解45次方程。韦达给出答案。
3.2. Fermat(1601-1665) 费马 数论之父
最高刑事法官 业余数学之王
- 解析几何(同笛卡尔) 代数用几何表达 几何用代数表达
- 概率论(与帕斯卡通信)
费马挚爱:数论 当时是小众学科,(帕斯卡不愿意)写信告诉法国科学家 无人感兴趣 额外贡献:光学费马原理
- 费马小定理: \(a^{p}\equiv a \mod p \quad p| \forall a \in \mathbb{Z}\)
- p 是平方和 \(\Leftrightarrow\) \(p=2, p=\equiv1\mod 4\)
- 大定理: 大于等于三没有整数解 只需要考虑 \(n=4,n=p\) 猜测他对于自己无穷递降法太自信于是写出“地方太小写不下”
证明 \(n=4\) 无非平凡解
- 不妨设 xy 互素
- 回顾勾股方程的本原解
3.3. Euler(1701-1783) 欧拉 最多产数学家
庞德丽亚金(双目失明) 算数的巅峰 伯努利的学生
圣彼得堡、柏林
分析进入数论 \(\zeta(s)=\sum\limits_{n>=1}\frac{1}{n^s}=\Pi_p \frac{1}{1-p^{-s}}\) 欧拉乘积 借此证明素数有无穷多 (有限乘积收敛,左边调和级数在1发散)
- \(\zeta(2)=1+=\frac{\pi^2}{6}\) 巴塞尔问题 \(\zeta(2n)=C_n\Pi^{2n}\)
黎曼将它变成复函数,解析开拓 3,5
- (数论的)欧拉定理: \(\phi(n)=\left\{ 0
模n的缩系
20岁干了很多事
3.4. 法国3L
Lagrange(1736-1813),Laplace,Legendre(1752-1833)
年纪轻轻的天才
3.4.1. Lagrange
自学数学成才 19 都灵教授 柏林科学院院士 拜伦普希金
- 1770:4平方定理 分析为什么次数小于4有根 分析求根公式 研究置换(为之后)
拉格朗日预解式 定理 \(\left| H \right|\left| \left| G \right| \right\) 元素的阶整除群的阶
3.4.2. Legendre
符号
\begin{equation} \label{eq:8} \left( \frac{a}{p} \right)= \begin{cases} 0 & p|a \\ 1 & a\equiv b^2 \mod p\\ -1& \text{else} \end{cases} \end{equation}后来被高斯重新做了 猜测:
- 二次互反律
一直苦恼于自己证明存在瑕疵
- 素数定理:
3.5. Gauss
(1777-1855) 数学王子
不世出的天才高斯登场了,可惜的是他基本只在25岁(1793)前研究数论,之后唯一关注的数论问题是上文素数定理 1801 《算数研究》 Disquisitiones Arithmeticae(基本是拉丁文写的最后学术专著)
- 第一本数论专著/教科书
- 先总结欧拉欧几里德中国算数,也就是初等数论到此总结完了
- 发明同余符号 \(a\equiv b \mod m \Leftrightarrow m|a-b\) 后一种是以前的写法
- 现代数论的开始(可以二次互反律)
- 证明二次互反律
二次型三次型-类数猜想~群(把之后概念拿过来就发现完美符合) 尺规正17边-费马素数 代数基本定理 复数引入数论
- 三平方和,从此可以立即推导出拉格朗日四次
184x
提升了数论的地位
费马无人问津,欧拉分析,因为高斯提升了数学家对数论的品味
3.6. Abel(1802-1829) Galois(1811-1832)
挪威 法国
受到时代巨大影响,他们的人生处在风雨飘摇岁月。。 拿破仑垮台(1814第一次下台)挪威丹麦, 丹麦支持拿破仑,之后将挪威让给瑞典。
当年很穷(之后因为发现石油富裕), 政治动荡。
3.7. Abel
穷苦家庭 15岁开始学数学,之后进展飞快。
良师指导 Holmboe , 发现才能很高,看欧拉拉格朗日拉普拉斯等等。 1820父亲去世,帮助继续读高中 深入唯一的大学当时是克里斯蒂安娜(首都,现在是奥斯陆)。 挪威政府资助游学
Crelle 柏林:1825 爱好者办杂志 6篇Abel 纯粹与应用数学
之前印刷 现存最古老杂质 19 德文 美国 anlysa of math
老师评价极高
研究五次方程; 主流数学椭圆函数。
雅可比 贫病 1828柏林给教授 病逝 Abel 积分范畴群引理判别 2002 Abel prize 挪威 百万 李 Lie 解析数论 近世代数C罗定理 身前身后名
高斯没看过
3.8. Galois
等刘维尔发掘的悲情人物
法国 路易18 共和党和保皇党斗争 王后镇 Banorg-la-Reine 一家是共和党人 父亲是市长。
12岁前母亲教导 路易大帝中学,最好的中学另一个是亨利四世中学 当时未学数学 人大附中
1823
1827学数学 一入侯门深似海, 参加考试 几个大学校 brand 巴黎高师、巴黎综合理工 当年politic 未考上
1829完成主要数学成功,发表连分数(已经蕴涵思想)。
5月提交五次方程: 柯西审稿退回,因为Abel,希望修改后重新。
7月父亲自杀因为他人羞辱。
12月通过会考录取高师(高师就在路易里面的几间房子) 数学认为表达不清但聪明其余科目不认可 再次提交傅里叶作为秘书1830.5.16去世,稿件丢失 奖给了Abel jacobi 椭圆函数
29 30
1831.1.17 泊松看不懂,认为没有完全展开
1815路易18上台24去世弟弟查理1937 七月革命推翻波旁王朝 菲利普国王上台
1831期间从事政治活动,被关监狱,长达10月
1832.5.30决斗31去世 写了一晚上信,总结自己贡献,寄给好朋友Chevalier,可以评价自己的成果 同其弟Alfred Galois 寄 写信给数学家,没有回信
1843.9.4 Liouville 报告提到伽罗瓦完全正确 原封不动发表自己杂志(法语的纯粹与应用杂志(第二古老数学杂志))
4. 数学理论
Galois 创立群论,同时在群论和域建立联系
4.1. 群论基础
群:一个数学结构——集合和运算(集合配上一个运算) \((G,\cdot)\)
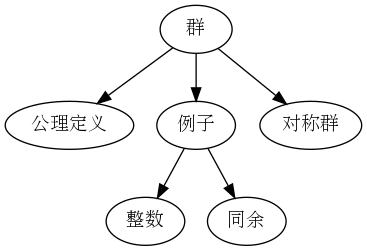
4.1.1. 群公理
即群的定义
- 结合律 \((ab)c=a(bc)\)
- 单位元 \(e\) \(ex=xe=x\)
- 逆元 \(ab=ba=e\)
满足上述公理为结构群
特别的,为什么是 结合
以前算得是数——需要交换 之后研究项…使用置换,置换的过程需要考虑次序——交换就不满足了 采用更(弱)一般的结合(结合在映射中也更普遍,讨论像对称置换更方便)
进一步定义:
- 满足交换律的群: 交换群=阿贝尔群(abelian group) 这个是小写
有限群 :元素个数有限
这里可以定义阶:
- 群的阶: \(|G|\) 元素个数
- 元素的阶: 满足 \(g^n=e\) 的最小整数 \(n\)
4.1.2. 例子
- 正整数加群 \((\mathbb{Z},+)\)
- 同余(将所有数除之后n得到的余数) \(\mathbb{Z}/n \mathbb{Z}=\{\bar{0},\bar{1},\cdots,\overline{n-1}\}\) 在加法下 \(\bar{a}+\bar{b}=\overline{a+b}\)
例子 1,2 是循环群。
- 正整数加群相等于 1 生成的无穷阶群 \(\left\langle 1 \right\rangle=\{\bar{1},\overline{1+1},\cdots\}\)
在乘法下( \(\bar{a}\cdot \bar{b}=\overline{ab}\) ) 去掉 \(\bar{0}\) 的子集 \((\mathbb{Z}/n \mathbb{Z})^{\times}\) 构成乘法下的群
首先,
\begin{gather*} (a,n)=1,(b,n)=1 \Rightarrow (ab,n)=1 \end{gather*}集合在乘法下是封闭的(也就是用教科书的话:乘法是其中的二元运算)
结合律; 单位元; 逆元:
\begin{gather*} (a,n)=1 \Leftrightarrow ua+vn=1, ua=1-vn \\ \Rightarrow \bar{u}\bar{a}=\bar{1} ,\bar{u}=\bar{a}^{-1} \end{gather*}使用了裴蜀定理对互素展开第一步
上述简单说明了它是群。
大小 \(|(\mathbb{Z}/ n \mathbb{Z})^{\times}|=\phi(n)\) ,其中 \(\phi\) 为 Euler 函数(给出了 1-n 素数的个数)
进一步,特殊情况 \(n=p\) 为素数
\begin{gather*} (\mathbb{Z}/p \mathbb{Z})^{\times} =\{a:0\leq a \leq p ,(a,p)=1\}\\ =\{a:0\((\mathbb{Z}/p \mathbb{Z},+,\cdot)\) 构成(有限)域
4.1.3. 有限生成交换群定理
?类似高等代数中(史密斯标准型定理)
有限生成交换群的结构定理
交换群 G
\begin{equation*} G\equiv \mathbb{Z}^r \oplus \mathbb{Z}/m_1 \mathbb{Z} \oplus \cdots \oplus \mathbb{Z}/m_s \mathbb{Z} , m_1|m_2|\cdots|m_s \end{equation*}?初等因子不变因子
?中国剩余定理将它们分开
4.1.4. 对称群
什么样的是对称群: n 个元素的置换群
(从运算表上可以轻易看出对称)
从 Lagragrane 开始 Galios 非常重要
大小-阶: \(|S_n|=n!\)
不再是初等数论同余的群, 和行列式(需要)相关的群。
4.1.4.1. 置换
表达置换
\begin{gather*} \sigma = \begin{pmatrix} 1&2&3&4&5&6&7&8\\ 8&3&4&2&6&5&1&7 \end{pmatrix} \\ \neq (8 3 4 2 6 5 1 7) \\ = (187)(234)(56) \end{gather*}两行式写成一行 轮换式
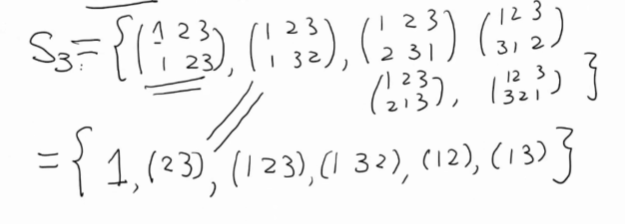
Figure 1: 举例 S3
4.1.4.2. 对称群 \(S_n\) 上的乘法
为映射的集合(置换相当于一个操作——映射)
查看结合
\begin{gather*} x_n={1,\cdots,n}\\ \sigma: x_n\rightarrow x_n ,\sigma \in S_n\\ \tau\sigma: x\overset{\sigma}{\rightarrow} x \overset{\tau}{\rightarrow} x\\ \sigma\tau: x\overset{\tau}{\rightarrow} x \overset{\sigma}{\rightarrow} x \end{gather*}(\(\sigma\) 为双射)
映射的复合满足结合律,但不必然满足交换律 如: \((13)(12)=(123)\neq(132)=(12)(13)\)
只有1,2是交换群
4.1.4.3. 对换
\((ij)\) 表示对换: \(i\) 到 \(j\), \(j\) 到 \(i\)
轮换变成对换:
\begin{equation*} (1\ 2\ 3\ \cdots\ n) = (1\ n)(1\ n-1)\cdots(1\ 2) \end{equation*}变为了 \(n-1\) 对换的乘积
任何一个置换是若干对换的乘积,组合的次数的奇偶性不变
(关联行列式的奇偶交错定义)
所有偶置换集合 \(A_n\subset S_n\) 称为 交错群
大小 \(1/2 n!\)
4.1.5. 矩阵群
称为典型群~一般线性群(行列式不为0,即可逆)、特殊线性群(行列式为1);正交群、酉群、辛群
4.2. 子群
符号表达: \(H\leq G\) (H 依然是个群) 对乘法和求逆封闭
研究 \(g\in G\) 包含 g 的最小子群是 \(\{ 1,g,\cdots,g^{k-1}\}\)
包含 g 也写作 a\(\left\langle g \right\rangle\) (g生成的群)。 此时, 原来 g 的阶就是群 \(\left\langle g \right\rangle\) 的阶
事实上,循环群只有两种(同构意义下),分别对应上面有限无限的整数和模剩余
4.3. Lagrange 定理
子群的阶一定整除大群的阶 (是大群阶的因子) \(\Rightarrow\) 元素的阶整除 G 的阶
陪集(元素平移)说明
证明思路:
构造陪集证明—— 要么重合要么不相交
\begin{gather*} G=\bigcup_{a\in G}aH\\ =a_1H \cdots a_s H \end{gather*}\(|G|=s|H|\)
特殊情况
4.3.1. Fermat 小定理
4.3.2. Euler 定理
4.3.3. 素数阶群
素数阶群都是循环群(只有一种结构)
4.4. 正规子群和商群
首先明确有陪集,陪集可以分左右
何时,对所有 g 左右陪集相等?相等就是正规子群。
\begin{gather*} gH=Hg\\ gN=Ng\\ \forall a g^{-1}ag\in N \end{gather*}商群 利用正规子群划分大群
\begin{gather*} G/N =\left\{ gN:g\in G \right\}\\ \bar{g}_1\bar{g}_2=\overline{g_1g_2}\\ g_1Ng_1N=g_1g_2N \end{gather*}4.4.1. 如何比较两个群
给出两者之间的映射,看这个映射的特点
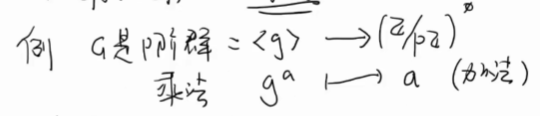
同态且是双射(既单又满)
(略)同态基本定理
4.4.2. 如何研究两个群
有限群情况:
4.4.2.1. 可解群—— Galois
如果可以拆出一串子列
\begin{equation*} 1=G_0 \triangleleft G_1 \triangleleft \cdots \triangleleft G_n =G \end{equation*}使得 \(G_{i+1}\triangleleft G_{i}\) 是 p 阶循环群 称 G
5. 域的理论
field
一个更熟悉的结构——更完整限制更好的存在
\((F,+,-,\times,|)\)
正统数论基于有理数域讨论
域至少两个元素 0,1 (一个元素的域)
线性代数是基于域的 (有理数的有限扩域)
5.1. 域扩张
\(F\subset E\) 中间 0,1 是同样的 , E 是 F 的扩域。 可以有乘法… 定义 \([E:F]:= \text{dim}_{F}E\)
定理 \(F\subset E\subset K\Rightarrow [K:F]=[K:E][E:F]\)
证明思路:

有趣的例子:
化零多项式

代数数、超越数
5.2. 尺规作图问题
直尺:没有刻度; 圆规。
给定原点和另一点 相当于 (1,0) 可以得到哪些点
光从几何上分析是困难的,不过首先要明白可以实现什么样的操作:
可以操作
做出的点集合 F 是一个域, 且 \(\mathbb{Q}\subset F \subset \mathbb{R}\) 新的点如何来
有限步-每一步得到一个(新的)域
画圆:开根号
新的域
\begin{equation*} L'= \begin{cases} L\\ L(\sqrt{\Delta}) \end{cases} \end{equation*}当且仅当必要条件
2
三大问题
高斯定理
费马素数
5.3. Gal 扩张
6. 环
内容包含平方和、 Gauss 素数
\begin{equation*} n=a^2+b^2=(a+b \mathrm{i})(a-b \mathrm{i}) \end{equation*}- 可逆元
- 素元
- 不可约元
定义一个绝对值、模
Footnotes:
老师讲的时候直接手写,很清晰,这里希望文档把这个作成一个近乎讲义可以直接看得学的内容